LEV: Die neuen Schwachstellen-Metriken in NIST CSWP 41 verständlich erklärt
Dieses Jahr werden die IT-Sicherheitsteams mit einer Flut neuer Sicherheitsrisiken überschwemmt. Bei der Behebung von Schwachstellen die Prioritäten richtig zu setzen, ist ein Dauerthema in der IT-Sicherheits- und Risikoanalyse. So müssen täglich neue Nadeln in einem Heuhaufen von Aufgaben gefunden werden. Zu den Faktoren, die dieses Problem noch verschärfen, gehören der Fachkräftemangel in der Cybersicherheit, neuartige Angriffstechniken und die zunehmende Offenlegung von CVEs (Common Vulnerabilities and Exposures).

Um diesem Bedarf an mehr Präzision und Effizienz gerecht zu werden, entstehen aktuell zahlreiche neue Priorisierungsmetriken. Nicht, dass mehr Risikoperspektiven etwas Schlechtes wären, aber die bereits überforderten Verteidigenden befinden sich in einer schwierigen Lage: Sie müssen sich entscheiden, ob sie weitermachen oder innehalten wollen, um den Wert neuer Metriken besser abzuschätzen.
Die im Mai 2025 vom NIST (National Institute of Standards and Technology) veröffentlichte Metrik Likely Exploited Vulnerabilities (LEV; Wahrscheinlich ausgenutzte Schwachstellen) konsolidiert historische Zeitreihen aus EPSS (Exploit Prediction Scoring System) und den Status der Ausnutzung in freier Wildbahn. Dadurch berechnet LEV um unter anderem eine aggregierte Risikobewertung. Dieser Artikel erläutert, was LEV ist und welche zusätzlichen Gleichungen in dem kürzlich veröffentlichten technischen Whitepaper des NIST (NIST CSWP 41) enthalten sind.
Der Grund für LEV (Likely Exploited Vulnerabilities)
LEV verwendet die historische EPSS-Zeitreihe einer CVE, um einen kumulativen Risikowert zu berechnen, der die Wahrscheinlichkeit darstellt, dass sie jemals aktiv ausgenutzt wurde. Aber worin unterscheidet sich dies von EPSS selbst? Ist EPSS, ein Modell aus dem Machine Learning (ML), das fast 1.500 Vorhersagemerkmale enthält, nicht gut genug?
Einige akademische Kritiken haben ergeben, dass EPSS kritische Schwachstellen übersehen kann. Die direkte Beobachtung historischer EPSS-Daten zeigt, dass die Werte für einen sehr kurzen Zeitraum (ein bis zwei Tage) in die Höhe schnellen können. Danach fallen sie meist wieder auf einen moderaten oder niedrigen Ausgangswert zurück. Das ist ein Problem für Sicherheitsverantwortliche, die EPSS einsetzen.
So spiegelt EPSS beispielsweise nicht wider, wie Cyberkriminelle vorgehen. Aus Branchenberichten geht hervor, dass sie Schwachstellen ausnutzen, wann und wo auch immer sie gefunden werden – sogar alte Schwachstellen. Mit anderen Worten: Angreifende verzichten nicht auf eine Schwachstelle, weil sie nicht aktuell ist. Die alleinige Nutzung aktueller EPSS-Werte kann riskant sein – selbst bei kürzlich entdeckten Schwachstellen. Verteidigende können dem begegnen, indem sie in ihrer Risikokalkulation immer den höchsten EPSS-Wert zugrunde legen: Aber eine weitere Schwachstelle bleibt bei den rohen EPSS-Werten bestehen: Statistisch gesehen sollte eine Ansammlung von mäßigen Wahrscheinlichkeitswerten auch eine hohe Wahrscheinlichkeit für das Eintreten eines Ereignisses bedeuten.
LEV behebt diese letzte Einschränkung durch die Berechnung einer kumulativen Wahrscheinlichkeit unter Verwendung der historischen EPSS-Daten der einzelnen CVEs. LEV wendet den üblichen produktbasierten Ansatz zur Berechnung der kumulativen Wahrscheinlichkeit des Eintretens mindestens eines Ereignisses unter mehreren unabhängigen Ereignissen an. Infolgedessen gelten CVEs, die selbst bei maximalem EPSS keine Warnungen ausgelöst haben, unter LEV nun als hochriskant.
Mathematische Variablen und Symbolreferenz
Diese Übersicht erklärt alle Variablen und mathematischen Symbole, die in den Gleichungen verwendet werden.
Variablen-Referenz
|
Symbol / Funktion |
Beschreibung |
Verwendet in |
|
v |
Eine Schwachstelle (z. B. ein CVE) |
Alle Gleichungen |
|
d |
Ein Datum ohne Zeitkomponente |
Alle Gleichungen |
|
d0 |
Erstes Datum mit EPSS-Daten für v |
Alle Gleichungen |
|
dn |
Das Analysedatum (normalerweise heute) |
LEV, erwartete Ausnutzung, kombinierte Wahrscheinlichkeit |
|
dkev |
Datum der letzten Aktualisierung der KEV-Liste (Known Exploited Vulnerabilities) |
KEV Ausgenutzt |
|
LEV (v,d0,dn) |
Kumulative Wahrscheinlichkeit der Ausnutzung von Schwachstelle v im Zeitraum d0 bis dn |
Alle Gleichungen |
|
EPSS (v,dn) |
EPSS-Punktzahl zum Zeitpunkt dn |
Komposit-Wahrscheinlichkeit |
|
KEV (v,dn) |
1.0 wenn v in KEV-Liste am Datum dn, sonst 0 |
Komposit-Wahrscheinlichkeit |
|
scopedcves |
CVEs mit d(0) ≤ dkev für KEV-Verfolgung |
KEV Ausgenutzt |
|
cves |
CVEs im Geltungsbereich mit d(0) ≤ dn |
Erwartete Ausnutzung |
Symbol-Referenz
|
Symbol |
Bezeichnung |
Bedeutung |
|
∀ |
Universeller Quantor |
„Für alle“ / „Für jeden“ ähnlich wie eine Programmierschleife |
|
Π |
Großes Pi |
Eine „Produktnotation“ für wiederholte Multiplikation über eine Folge, ähnlich wie ∑ für wiederholte Addition steht. |
|
∑ |
Großes Sigma |
Ein Summenzeichen für die wiederholte Addition über eine Sequenz. |
|
∈ |
Element von |
„Ist ein Element von“ / „gehört zu“. Bezeichnet die Zugehörigkeit zu einer Menge. |
Funktionsweise der LEV-Gleichungen
Die LEV-Metrik wird im „Cybersecurity White Paper 41” (CSWP 41) des NIST als eine untere Grenze der Wahrscheinlichkeit beschrieben, dass eine Schwachstelle ausgenutzt wurde. Sie berechnet die kumulative Wahrscheinlichkeit, dass eine Schwachstelle innerhalb eines bestimmten Zeitfensters mindestens einmal ausgenutzt wurde. Es gibt zwei ähnliche Gleichungen, LEV und LEV2. Die erste wurde optimiert, um die CPU-Last zu verringern.
In beiden Gleichungen, LEV und LEV2, steht jeder Term, der mit der Produktnotation Π multipliziert wird, für die Wahrscheinlichkeit, dass in diesem Zeitfenster keine Schwachstelle ausgenutzt wurde. Man erhält die kumulative Wahrscheinlichkeit, dass nie eine Ausnutzung stattgefunden hat. Subtrahiert man das Ergebnis von 1, erhält man die Wahrscheinlichkeit, dass mindestens eine Ausbeutung während des Zeitfensters stattgefunden hat.
Die beiden LEV-Gleichungen werden im Folgenden beschrieben:
Die leistungsoptimierte LEV-Gleichung
LEV verwendet die historischen EPSS-Werte eines CVE, die alle 30 Tage ermittelt werden (epss(vi, di) ), und eine ausgleichende Gewichtung für Beobachtungszeiträume unter 30 Tagen (dn < 30)
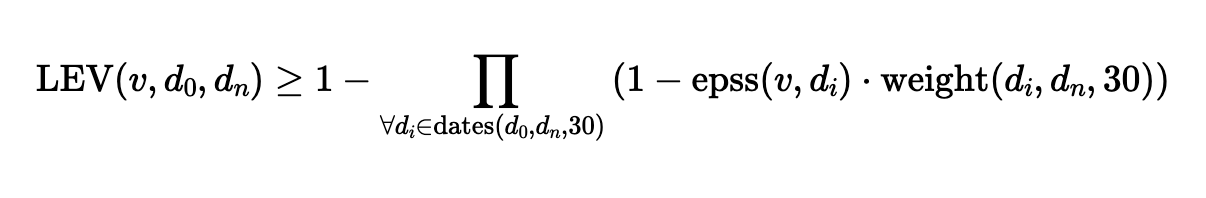
Die im NIST CSWP 41 vorgeschlagene LEV-Gleichung
Die hochauflösende LEV2-Gleichung
LEV2 verwendet die gesamte historische EPSS-Zeitreihe, anstatt alle 30 Tage eine Stichprobe der Werte zu nehmen. LEV2 gewichtet die täglichen Werte, indem es diese durch die Dauer des EPSS-Fensters (30 Tage) teilt. LEV2 erhöht die zeitliche Auflösung und führt zu einer zuverlässigeren Bewertung, da kurze Ausbrüche hoher EPSS-Werte nicht wie bei der oben dargestellten LEV-Gleichung übersprungen werden können. Jeder tägliche EPSS-Wert wird mit 1/30 skaliert, um eine einheitliche Risikodichte über den gesamten Datumsbereich zu erhalten.
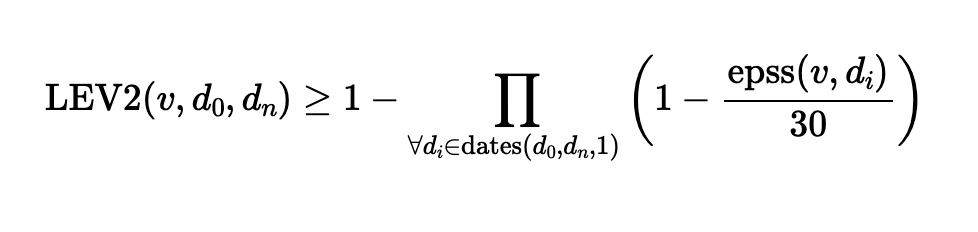
Die im NIST CSWP 41 vorgeschlagene LEV2-Gleichung
Die ergänzenden Gleichungen
Dieser Abschnitt stellt zusätzliche Gleichungen aus dem LEV-Whitepaper des NIST vor, samt Aufbau und möglichen Anwendungen.
Berechnung eines zusammengesetzten Risiko-Scores
Die im LEV-Whitepaper des NIST beschriebene ergänzende Metrik für die Wahrscheinlichkeit wählt einfach das stärkste verfügbare Signal aus den drei Ausnutzungsindikatoren EPSS, Einbeziehung in den KEV-Katalog der CISA (Cybersecurity and Infrastructure Security Agency) und LEV aus.
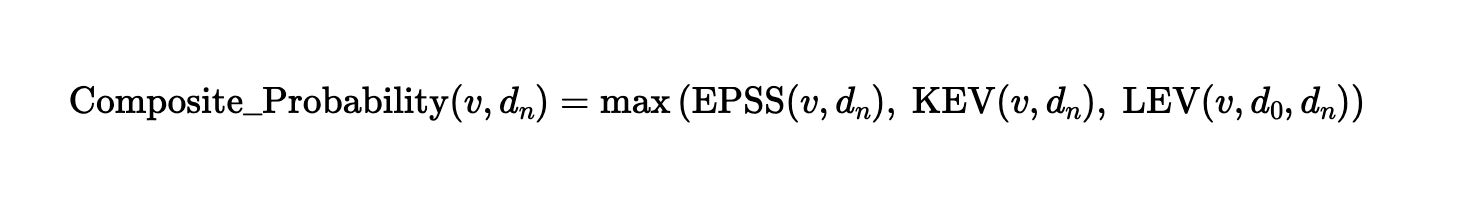
Die im NIST CSWP 41 vorgeschlagene Gleichung für die zusammengesetzte Wahrscheinlichkeit, den „Composite Risk Score“
Durch die Auswahl des aussagekräftigsten Signals unterstützt Composite Probability die Priorisierung von Schwachstellen und reduziert blinde Flecken, bei denen ein Signal unvollständig oder veraltet sein kann. Dies ist besonders wertvoll für die Priorisierung von Abhilfemaßnahmen in großen Unternehmens-Programmen zur Verwaltung von Schwachstellen, bei denen die Entscheidung, was zuerst behoben werden soll, eine kritische Herausforderung darstellt.
Schätzung der Gesamtzahl der ausgenutzten CVEs
Das Whitepaper des NIST schlägt auch eine Methode vor, um die Gesamtzahl der ausgenutzten CVEs während eines bestimmten Zeitfensters zu schätzen und wie man den Umfang eines Verzeichnisses bekannter ausgenutzter Schwachstellen abschätzen kann.
Die „Expected Exploited“-Berechnung
Die „Expected Exploited“-Metrik ist eine Schätzung der Anzahl der ausgenutzten CVEs innerhalb eines bestimmten Zeitfensters durch einfache Summierung aller LEV-Wahrscheinlichkeiten aus einem Satz von skalierten Schwachstellen. Die Gleichung „Expected Exploited“ wendet einfach die Summe (∑) aller LEV-Wahrscheinlichkeiten für einen Satz von CVEs an, um die Gesamtzahl der wahrscheinlichen Ereignisse zu schätzen. Obwohl sie im NIST CSWP 41 als untere (konservative) Schätzung beschrieben wird, ist es methodisch unüblich, diese einfache Technik als untere Grenze zu betrachten. In der Wahrscheinlichkeitstheorie ist es ein grundlegendes Prinzip, dass die erwartete Anzahl von Ereignissen gleich der Summe der einzelnen Ereigniswahrscheinlichkeiten ist.
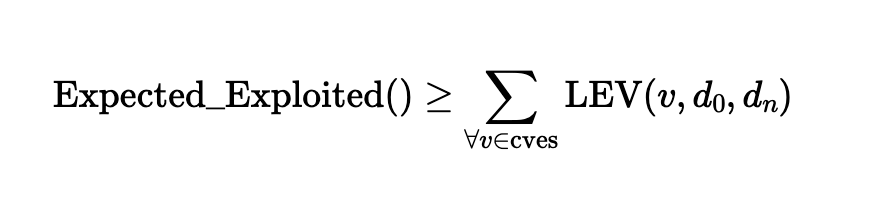
Die im NIST CSWP 41 vorgeschlagene „Expected Exploited“-Gleichung
Die KEV Exploited-Berechnung
Die KEV Exploited-Metrik schätzt, wie viele Schwachstellen in einem KEV-Katalog wie dem CISA KEV fehlen. Die Quantifizierung der Lücke zwischen „Expected Exploited“ und „KEV Exploited“ gibt Aufschluss über die potenzielle Untererfassung einer KEV-Liste. Die Gleichung basiert wie die „Expected Exploited“-Berechnung auf der Summierung aller Wahrscheinlichkeiten.
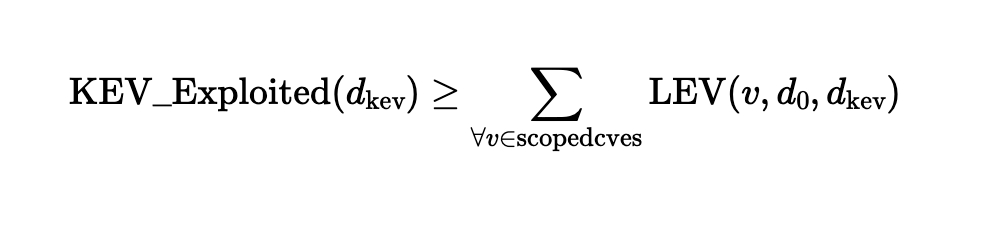
Die in NIST CSWP 41 vorgeschlagene KEV Exploited-Gleichung
Anwendungsbeispiele von LEV
Folgende Beispiele zeigen, wie LEV Schwachstellenmanagement-Programme unterstützen kann. Die ergänzende Composite Probability-Gleichung eignet sich am besten, um den Beitrag von LEV zu einer umfassenderen CVE-Risikoanalyse zu veranschaulichen. Daher verwenden alle nachfolgenden statistischen Beobachtungen die zusammengesetzte Wahrscheinlichkeit, sofern nicht anders angegeben.
Die geschätzte Gesamtzahl der ausgenutzten CVEs
Wenn man alle CVEs seit etwa 1980 (273.979) betrachtet, zeigt die LEV-Metrik „Expected Exploited“, dass 14,6 % aller CVEs (39.925) wahrscheinlich real ausgenutzt wurden. Das impliziert, dass die überwiegende Mehrheit der Ausnutzungsaktivitäten in keiner bekannten KEV-Liste erfasst ist (z. B. enthielt CISA KEV zum Zeitpunkt der Berechnung 1.228). Allerdings berücksichtigt Expected Exploited nicht, wie viele einzelne CVEs bei verschiedenen EPSS-Schwellenwerten aufgedeckt werden können.
Die Anzahl der aufgedeckten Hochrisiko-CVEs
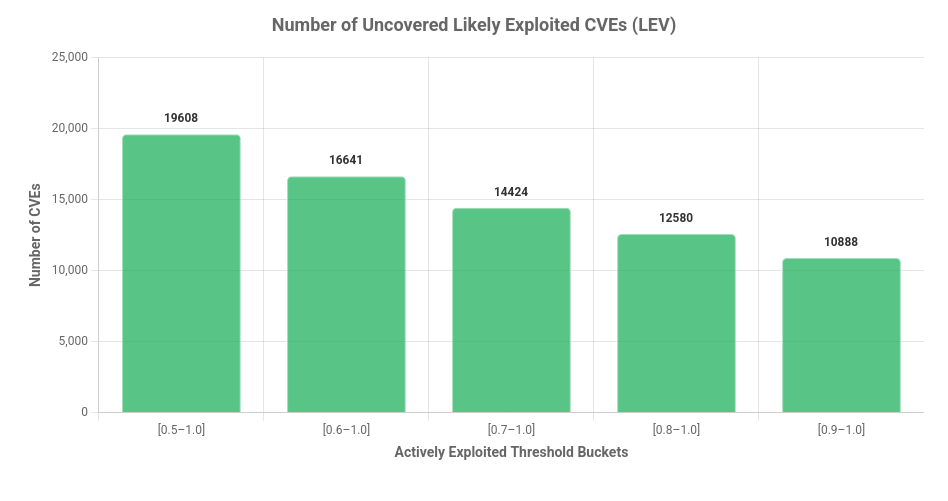
Um den Einfluss von LEV auf die Risikobewertung und Priorisierung in Organisationen zu beurteilen, ist es sinnvoll, die Anzahl der dadurch identifizierten Hochrisiko-CVEs zu betrachten. Das folgende Diagramm zeigt, wie viele CVEs in einer Risikoanalyse bei verschiedenen Schwellenwerten über 50 Prozent der zusammengesetzten Wahrscheinlichkeit sichtbar werden würden.
Die Anzahl der CVEs, die unter Verwendung der Metrik Composite Probability (Zusammengesetzte Wahrscheinlichkeit) auf verschiedenen Wahrscheinlichkeitsstufen auf ein hohes Risiko heraufgesetzt wurden
Visualisierung der Risikomigration mit Composite Probability
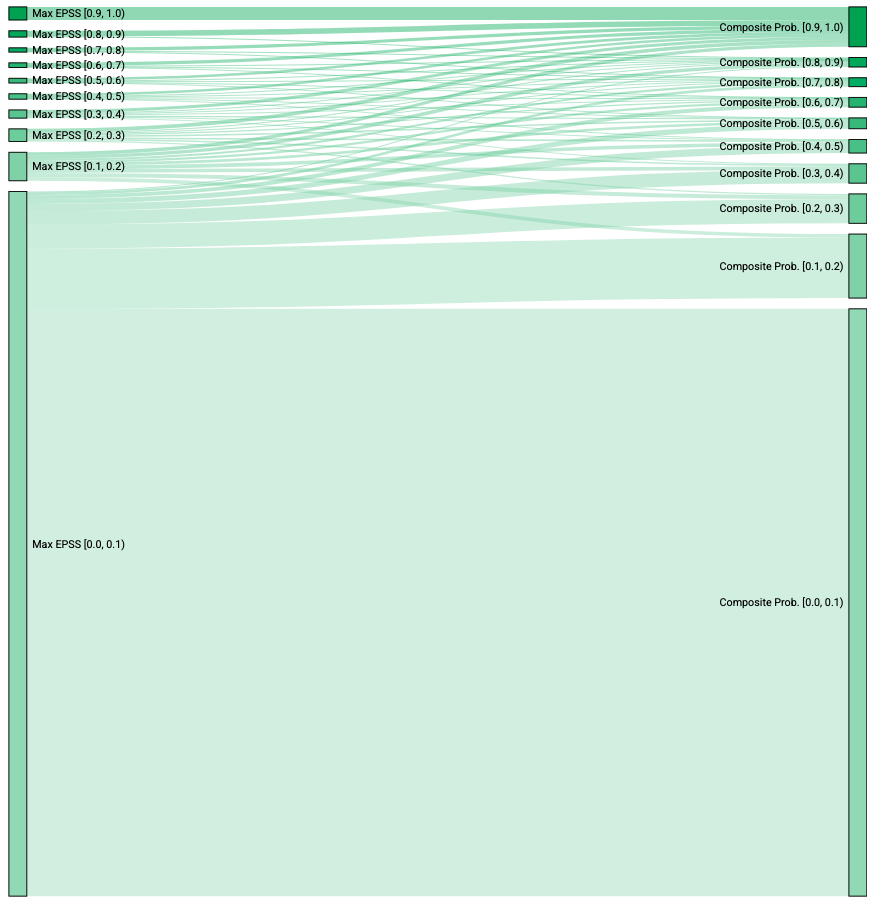
Das Sankey-Diagramm vergleicht, wie viele CVEs sich in jeder Risikostufe befinden, wenn die maximale EPSS (links) mit der zusammengesetzten Wahrscheinlichkeit von LEV (rechts) verglichen wird. Da die zusammengesetzte Wahrscheinlichkeit verwendet wird, wandern CVEs in der Regel nicht in niedrigere Risikostufen. Das Diagramm zeigt eine signifikante Migration vom niedrigsten Risikobereich zu höheren Bereichen und einen Anstieg für alle anderen Gruppen, wenn die Composite Probability zur Risikoabschätzung verwendet wird.
Sankey-Diagramm, das die Migration von CVEs zwischen Risikobereichen bei der Verwendung von EPSS und der LEV-Metrik „Composite Probability“ zeigt
Einschränkungen und Kritikpunkte an LEV
Die LEV-Metrik bietet zwar wertvolle Einblicke, dennoch sollten ihre Annahmen und potenziellen Schwächen kritisch betrachtet werden:
- Das LEV-Whitepaper enthält keine empirische Validierung oder Vergleiche mit anderen statistischen Modellen. Ein frequentistischer Ansatz mit produktbasierter Wahrscheinlichkeit ist jedoch eine bewährte Methode zur Berechnung der kumulativen Wahrscheinlichkeit für eine Reihe unabhängiger Ereignisse.
- LEV wird als eine untere Wahrscheinlichkeitsgrenze beschrieben. Es fehlen jedoch akademische Belege dafür, dass die im NIST CSWP 41 beschriebenen mathematischen Modelle tatsächlich konservative Schätzungen von Untergrenzen darstellen.
- LEV ist an sich kein undurchsichtiges Vorhersagesystem, aber es basiert auf EPSS, das kein vollständig öffentliches Modell ist. LEV behebt zwar einige potenzielle Schwachstellen, ist aber von EPSS abhängig. In dem Maße, wie EPSS verbessert wird, wird auch LEV von diesen Verbesserungen profitieren. Zum Beispiel hat EPSS v4 Malware-Aktivitäten und Endpunkt-Erkennungen zu seiner „Grundwahrheit“ der realen Ausnutzung hinzugefügt. Dies reduziert die frühere Verzerrung zugunsten von netzwerkbasierten Schwachstellen.
- Sicherheitsverantwortliche sollten sich bei der Priorisierung von Schwachstellen nicht zu sehr auf LEV, EPSS oder CVSS verlassen. Zwar sind Beweise für eine aktive Ausnutzung das stärkste Risikosignal, doch kommen diese Beweise oft erst im Nachhinein – zu spät um eine rechtzeitige Reaktion zu ermöglichen.
Zusammenfassung
LEV bietet einige Verbesserungen bei der Schwachstellen-Priorisierung, indem historische EPSS-Signale zu einer kumulativen Ausnutzungswahrscheinlichkeit zusammengefasst werden. Dieser Ansatz erhöht die Sichtbarkeit von CVEs mit einer historischen Dauer und moderaten EPSS-Werten. Die vielleicht nützlichste Kennzahl ist die vorgeschlagene zusammengesetzte Wahrscheinlichkeit, die das stärkste Signal aus LEV, EPSS und dem CISA KEV-Ausnutzungsstatus auswählt.
Josephs Karriere im Bereich IT und Cybersicherheit ist von Vielfalt und Leidenschaft geprägt. Sie begann in den späten 1980er Jahren mit der Arbeit an einem IBM PS/2, der Montage von PCs und der Programmierung in C++.
Er studierte Computer- und Systemtechnik, Anthropologie und erwarb einen MBA mit Schwerpunkt Technologieprognose.
Josephs Fachgebiete umfassen Datenanalyse, Softwareentwicklung und insbesondere IT-Sicherheit in Unternehmen. Er ist Experte für Schwachstellenmanagement, Verschlüsselung und Penetrationstests.